Discrete Math dạy những gì? Và học Discrete Math online ở đâu?
07 Mar 2020
・

Chào mừng các bạn đến với tập tiếp theo, và cũng là tập cuối cùng (tạm thời là vậy) của chuyên mục Discrete Math.

Ở tập trước, tui đã giải thích Discrete Math là gì. Tại sao học CS lại phải học Discrete Math?

Tập này tui giải quyết nốt 2 câu hỏi dưới đây nhé:

  1. DM dạy những gì?
  2. Học Discrete Math Online

1. Discrete Math dạy những gì?

Discrete Math chia thành nhiều chủ đề và có nhiều ứng dụng trong các nhiều mặt của CS. Dưới đây chỉ tui trích ra 4 chủ đề quan trọng để giải thích cùng các ứng dụng tiêu biểu hen.

3.1 Proofs (Chứng minh)

Thông thường Proof sẽ là chủ đề đầu tiên trong các khóa học Discrete Math, vì đây là tiền đề xây dựng logic toán, và nền tảng để học các chủ đề sau.

Trong Proofs, bạn sẽ được học cách tận dụng logic toán để chứng minh các định lý toán học (theorems), sau đó là thuật toán (algorithmss). Bạn bắt đầu bằng cách chứng minh các câu hỏi được đặt ra là đúng hay sai, vấn đề được đặt ra có thể hay không thể. Quan trọng hơm? Có chứ.

Một ví dụ kinh điển thường được đưa ra khi tìm hiểu vấn đề này là một trò chơi có tên gọi 14-15 puzzle (hoặc 15 puzzle). Thử thách ở đây là làm sao để cho A trở thành B. Những năm cuối 1800s, dân Bắc Mỹ và Châu Âu cũng đắm đuối với trò chơi này, và khắp nơi có giăng ra nhiều phần thưởng hiện kim hấp dẫn. Discrete Math là gì?

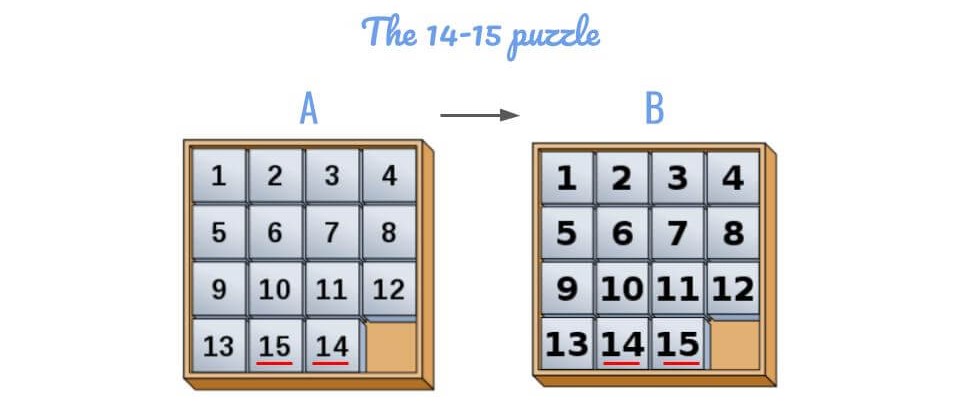
Bạn nào hứng thú có thể giải thử. Spoiler Alert! Nếu dùng logic, bạn có thể tránh khỏi việc lãng phí vài giờ, hoặc vài ngày giải puzzle này vì các nhà toán học đã chứng minh được điều này là không thể. Trong discrete math, đây được gọi là bất biến (invariance).

Invariance ngoài việc giúp bạn đỡ tốn não và thời gian giải puzzle trên, thì còn được áp dụng để tránh các lỗ hổng thiết kế, đảm bảo an toàn trong vận hành. Ví dụ như việc sử dụng bất biến để đảm bảo an toàn cho quy trình giảm độ cao của máy bay không được giảm quá 300m (chẳng hạn) khi thiết bị hạ cánh chưa được khởi động. Hoặc để đảm bảo nhiệt độ của lò phản ứng hạt nhân không bao giờ vượt quá giới hạn nguy hiểm dẫn đến tai nạn nóng chảy hạt nhân và làm hư trái đất.

3.2 Graph theory (Lý thuyết đồ thị)

Nhớ hồi cấp 1 mấy đứa trong lớp hay đố nhau:

Đây cũng thường là một ví dụ hay được đưa ra khi học Graph theory. Bây giờ sử dụng Proof và Graph theory rồi mới thấy đúng là một thời tuổi thơ non dại.

Nói về áp dụng thì có thể nói Graph theory được áp dụng vô cùng rộng rãi để tối ưu hiệu suất, đặc biệt có ích cho các vấn đề logistics.

Tui là tui thích học Graph theory nhất, vì dễ dàng có thể thấy ứng dụng của graph theory trong đời sống hằng ngày.

Graph theory đưa ra câu trả lời cho các bài toán diện nhỏ như thiết kế computer network trong 1 công ty, cho đến diện khổng lồ như thiết kế đường metro, hay mạng lưới điện nước toàn thành phố. Cá nhân bạn cũng có thể áp dụng để trả lời những câu hỏi hằng ngày như đường nào để đi mua trà sữa nhanh nhứt? Mỗi lần bạn bấm nút Get Directions trong Google Maps là bạn đang kích hoạt thuật toán của Graph Theory đó.

3.3 Number Theory (Lý thuyết số)

Number Theory là ngành nghiên cứu về số nguyên, đặc biệt là số nguyên tố (prime number). Đây chính là nền tảng để xây dựng nên một đế chế Cryptography (mật mã học) - a.k.a anh hùng cứu vớt Quyền riêng tư và An toàn giữa một rừng rậm mang tên internet-ngày-nay.

Học Number theory và Crytography mới biết các bác toán học khéo léo như thế nào trong việc mã hóa và cất dấu thông tin.

Bạn tỏ tình với crush qua whatsapp. Bạn và crush mỗi người cần có một chiếc chìa khóa riêng biệt để khóa và mở bức thư đó. Thử thách ở đây là whatsapp phải mã hóa thế nào để tin nhắn có thể đáp ứng được 2 cái chìa khóa đó, để cả thế giới (trừ 2 bạn) không biết tin nhắn đó chứa gì?

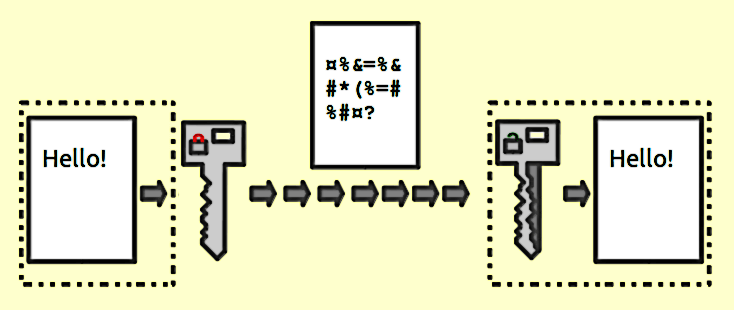
Hint: câu trả lời sẽ liên quan đến rất nhiều số nguyên, số nguyên tố, các phép nhân chia và rất nhiều định lý hại não. Hỏi sao hacker đều là những thần đồng? Tuy khó nhưng chủ đề này cũng rất thú vị và thực tế vì mình có thể hiểu được cơ chế bảo mật của những platform mình sử dụng hằng ngày hằng ngày. Không chỉ trong được áp dụng trong việc bảo mật tin nhắn hay email, Number Theory còn giúp cho việc mua bán online trở nên mượt mà và an tâm hơn. Mỗi lần bạn cần cà thẻ mua đồ trên tiki, thanh toán với visa, paypal hay sử dụng tài khoản icloud, bạn đều đang đặt cược, à không đặt niềm tin :> vào những thuật toán của Number Theory.

3.4 Combinatorics (Toán học tổ hợp)

Như number theory, combinatorics cũng liên quan đến rất nhiều số và phép nhân chia nhưng chủ yếu để áp dụng cho việc đếm tất cả các trường hợp có thể xảy ra và từ đó tính toán tính khả thi.

Ví dụ như ai đó lấy trộm chiếc iphone của bạn và đang thử hack cái mật khẩu 6 chữ số để truy cập vào máy. Apple cài đặt 10 lần thử trước khi khóa máy vĩnh viễn hoặc xóa toàn bộ thông tin trong máy. Khả năng tên trộm có thể hack vào điện thoại trước khi bị Apple khóa Iphone vĩnh viễn là bao nhiêu phần trăm?

Mình có 10 số (0-9) để nhập vào 6 chỗ trống. Vậy khả năng tên kia có thể hack vào tài khoản của bạn là: 10 lần thử / (10^6) khả năng = 1/100000 = 0.001%

Các công ty công nghệ áp dụng Combinatorics để thiết kế hệ thống password bảo mật và an toàn. Với Apple trong trường hợp trên, khả năng để thông tin của bạn bị lộ là 0.001%. Còn với bạn, nếu bị mất iphone thì khả năng mất dữ liệu là 99.999%. Bài học rút ra là dù thế nào đi chăng nữa thì cũng phải cẩn thận và nên đi backup lên iCloud liền.

Combinatorics sẽ giúp bạn có nền tảng để trả lời những câu hỏi dạng vậy, tất nhiên là ở độ phức tạp cao hơn nhiều.

-

Đây chỉ là những chủ đề tiêu biểu của DM thôi, tùy mỗi chương trình và giáo trình sẽ có thêm nhiều chủ đề khác nhau nữa. Lúc mới học Discrete Math tui cũng lo vì giờ đã quên hết toán phổ thông rồi, nhưng tin vui là bạn không cần nhớ gì hết để bắt đầu. Thiệt! Khi học, bạn sẽ được gợi lại một số chủ đề được học hồi xưa như chứng minh định lý, áp dụng True/False khi tương tác giữa các tập hợp con (set), có một số kiến thức liên quan đến ma trận, vi tích phân, thống kê nhưng thông thường giáo trình sẽ build từ định nghĩa cơ bản nên rất dễ bắt theo.

Ấn tượng đầu tiên khi tui học Discrete Math là ở cách bóc tách vấn đề và khả năng nhìn sâu hơn vào nền tảng của toán học nói riêng và khoa học nói chung. Thi thoảng ngồi thực hành giải proof tui cũng có cảm giác đang thực hành khoa học, một cảm giác khá yomost các bác ạ. Khi đi sâu hơn và bắt đầu hiểu dần thì sẽ thấy Discrete math đúng là toán đời thực - vì qua đó bạn sẽ được rèn luyện về logic nói chung, logic tính toán, tối ưu nói riêng và có thể thấy và áp dụng trong đời sống hằng ngày.

4. Học Discrete Math Online

Trên mạng (Youtube, Coursera, Edex, … ) có rất nhiều khóa học Discrete Math. Mỗi khóa học sẽ cần khoảng 40 giờ nghe giảng + 20 giờ tự học (giao động tùy vào độ chăm của bạn) và đa phần đều miễn phí. Giữa nhiều lựa chọn, tui đi loanh quanh trên các diễn đàn như Quora, Reddit để tìm 1 chương trình học ổn thì đã được các Professor và các anh chị tốt nghiệp Computer Science dẫn đến một khóa học Discrete Math được cho là kinh điển nhất của MIT Open Course Ware.

Bạn có thể nghe thử bài đầu để được sự hay ho của Discrete Math và độ cuốn hút của lecturer là thầy Tom - giờ hiện là CEO của Akamai Technologies. Tui nghe xong bài này là lập tức muốn quay về ghế nhà trường liền.

Ngoài các video trên youtube, MIT có cung cấp đầy đủ tài liệu sách giáo khoa, handouts, bài tập, bài thi và bài giải miễn phí trên website khóa học. SGK do thầy Tom và đồng nghiệp biên soạn riêng, đọc rất hay, nhiều ví dụ thông minh và dí dỏm. Có một vài lecture khá khó nuốt nên việc đọc sách sẽ hỗ trợ bạn rất nhiều trong việc theo sát khóa học.

Discrete Math by MIT Open Course Ware:

Ngoài khóa này thì tui có nghe thêm một số giảng viên khác trên youtube để hiểu sâu hơn, link dưới đây:

Dưới đây tui bonus thêm các link của những nguồn giải thích rất hay và sâu hơn về khái niệm Discrete Math. Mỗi bài chỉ tốn tầm 5-10’ nghe/đọc thôi nên các bạn có thể tham khảo nhanh:

Vậy hen, mong các bạn có thể hiểu hơn về Discrete Math qua bài viết này. Happy study!